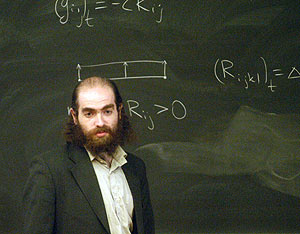Nov 28 2023
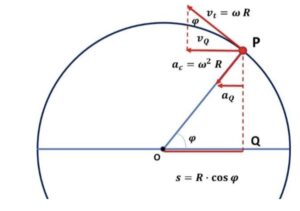
Formulario sui moti piani
MOTO PARABOLICO Il moto parabolico consiste nel lanciare un oggetto (proiettile) ad un angolo compreso tra 0° e 90° rispetto al piano orizzontale (schematizzato con l’asse X), in presenza di un campo gravitazionale diretto lungo l’asse verticale (Y). Nella figura successiva, V0 è la velocità iniziale (vettore) ed è l’“alzo”. La distanza tra l’origine e …
Mar 09 2024
Progetto STEM tra ISIS Pacioli e IC Tenente De Rosa
Le slide da consultare per l’attività sono disponibili di seguito. Per scaricare la versione *.ppt clicca QUI.
Dic 08 2023
Simulazioni scientifiche da browser
Il sito è https://phet.colorado.edu/it, anche il italiano! Su questo interessante sito è possibile trovare simulazioni di esperimenti fisici o altre situazioni scientifiche. Clicca QUI per accedere alla pagina delle simulazioni.
Nov 23 2023
Grigorij Jakovlevič Perelman
Ha risolto uno dei più grandi problemi matematici al Mondo.Visto e fotografato nella metropolitana della città da un blogger russo, appare nelle immagini fotografiche con i capelli arruffati, la barba incolta e vecchie scarpe quasi come fosse un senzatetto o un mendicante.L’Istituto Clay annunciò l’assegnazione del premio di 1 milione di dollari a Perelman relativo …
Nov 23 2023
Teorema di Napoleone
Nella geometria elementare del piano, stabilisce che se sui lati di un qualsiasi triangolo ABC si costruiscono, esternamente a esso, tre triangoli equilateri, i centri di questi ultimi sono i vertici di un triangolo equilatero, detto triangolo di Napoleone.